![\[
u_t = F(x,t,u,u_x,u_{xx}),
\]](pcp571s97_1.gif)
![\[
u_t = F(x,t,u,u_x,u_{xx}),
\]](pcp571s97_1.gif)
where
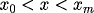 ,
,
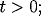
![\[
F(x,t,u,u_x,u_{xx}) = a(x) u_{xx} + b(x) u_x + c(x) u + d(x,t).
\]](pcp571s97_4.gif)
Consider the special test example with spatially variable coefficients,
![\[
a(x) = 5.712*x_m^2/(1 + x^2),
\]](pcp571s97_5.gif)
![\[
b(x) =
0.571 (x-x_0) (x_m-x) (1-0.648 (x-x_0)/(x_m-x_0)),
\]](pcp571s97_6.gif)
![\[
c(x) = 0.387 (x-x0) (x_m-x)/((x_m-x_0)^2 + x^2),
\]](pcp571s97_7.gif)
![\[
d(x,t) = -0.067 \exp(-0.571t) \sin(\pi x/(x_m-x_0)),
\]](pcp571s97_8.gif)
on
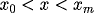 , with initial conditions:
, with initial conditions:
![\[
u(x,0) = 100 \exp(-0.17 (x-x_0) (x_m-x)) /\sqrt{\pi/0.571} ,
\]](pcp571s97_10.gif)
on
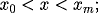 and boundary conditions:
and boundary conditions:
![\[
u(x_0,t) = 3.7t/(1+t^2),
\]](pcp571s97_12.gif)
![\[
u(x_m,t) = 4.2 \exp(-0.5t^2),
\]](pcp571s97_13.gif)
for t > 0
with
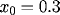 ,
,
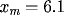 , m = 11,
n= 101 and mesh requirements,
, m = 11,
n= 101 and mesh requirements,
![\[ h = (x_m-x_0)/m \]](pcp571s97_16.gif) ,
,
![\[ \widehat{r} \equiv \widehat{a} k/h^2 = 0.01 \]](pcp571s97_17.gif) ,
,
where
![$ \widehat{a}=\min[a(x)] $](pcp571s97_18.gif) ,
,
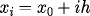 for i=0 to m,
for i=0 to m,
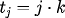 for j=0 to n.
Use an
for j=0 to n.
Use an
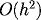 high order Forward Finite Difference
approximation for
high order Forward Finite Difference
approximation for
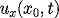 .
If your method needs corner values, i.e.,
.
If your method needs corner values, i.e.,
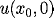 and
and
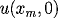 , use the
average values of the boundary and initial conditions.
Warning: Do not write your code only for numerical values
given here, but write it more generally and not just for this
test case.
, use the
average values of the boundary and initial conditions.
Warning: Do not write your code only for numerical values
given here, but write it more generally and not just for this
test case.
![\[
U_{i,j+1} = U_{ij} + k F(x_i,t_j,U_{ij},DU_{ij},DDU_{ij}),
\]](pcp571s97_25.gif)
where here
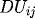 and
and
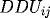 are the
Central Finite Difference (CFD) approximations using
are the
Central Finite Difference (CFD) approximations using
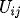 corresponding
to the derivatives
corresponding
to the derivatives
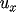 and
and
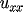 , respectively.
, respectively.
The Crank-Nicolson Implicit Method (CNIM) is
![\[
U_{i,j+1} = U_{ij} + k F(x_i,t_{j+\frac{1}{2}},CU_{ij},DCU_{ij},DDCU_{ij}),
\]](pcp571s97_31.gif)
where
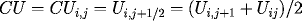 and the corresponding
CFD derivatives are
and the corresponding
CFD derivatives are
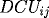 and
and
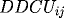 ,
all using
,
all using
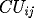 as discrete
values. Use the Thomas Tridiagonal Solver Algorithm to solve.
as discrete
values. Use the Thomas Tridiagonal Solver Algorithm to solve.
The 4th order Runge-Kutta Explicit method (RKEM) (modified PPDE for this Computer Problem from the 4th order RKEM ODE method) is written,
![\[
U_{i,j+1} = U_{ij} + k (RK1+2 (RK2+RK3)+RK4)_{ij}/6,
\]](pcp571s97_36.gif)
for interior points, where
![\[
RK1_{ij} = F(x_i,t_j,RU1_{ij},DRU1_{ij},DDRU1_{ij}),
\]](pcp571s97_37.gif)
with
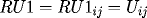 with corresponding
derivatives
with corresponding
derivatives
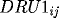 and
and
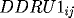 (all indexed at (i,j)),
(all indexed at (i,j)),
![\[
RK2_{ij} = F(x_i,t_{j+\frac{1}{2}},RU2_{ij},DRU2_{ij},DDRU2_{ij}),
\]](pcp571s97_41.gif)
with
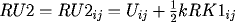 and
corresponding derivatives
and
corresponding derivatives
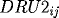 and
and
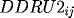 ,
,
![\[
RK3_{ij} = F(x_i,t_{j+\frac{1}{2}},RU3_{ij},DRU3_{ij},DDRU3_{ij}),
\]](pcp571s97_45.gif)
with
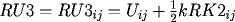 and
corresponding derivatives
and
corresponding derivatives
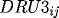 and
and
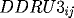 , and
, and
![\[
RK4_{ij} = F(x_i,t_{j+1},RU4_{ij},DRU4_{ij},DDRU4_{ij}),
\]](pcp571s97_49.gif)
with
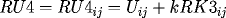 and
corresponding
derivatives
and
corresponding
derivatives
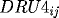 and
and
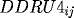 ,
using
,
using
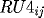 as discrete values.
Each
as discrete values.
Each
![$ DRU[p]_{ij} $](pcp571s97_54.gif) should satisfy derivative boundary
conditions
where they are specified, for [p] = 1, 2, 3, and 4.
should satisfy derivative boundary
conditions
where they are specified, for [p] = 1, 2, 3, and 4.
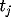
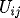 , while RELDIF[EEM] &
RELDIF[CNIM] are the relative difference of
the first two methods compared to RKEM, i.e.,
, while RELDIF[EEM] &
RELDIF[CNIM] are the relative difference of
the first two methods compared to RKEM, i.e.,
![$ RKEM[U] \neq 0 $](pcp571s97_57.gif) . Also print out the outputted
locations,
. Also print out the outputted
locations,
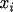 , at least once at the beginning of the
tabulated numerical output. In
addition, report the timings in seconds for each method, counting
common initializations of terms like coefficient arrays
for {a, b, c, d} and output.
, at least once at the beginning of the
tabulated numerical output. In
addition, report the timings in seconds for each method, counting
common initializations of terms like coefficient arrays
for {a, b, c, d} and output.
1) Compute once and store the spatially dependent coefficients in an array to use in all time steps.
2) Avoid calculating items like constant expressions in loops, but keep code general.
Added Note: These methods can also be used for nonlinear PPDEs,
directly for EEM and RKEM, but with a predictor-corrector modification
for CNIM.
Email Comments or Questions to hanson@uic.edu