The Principles of Polynomial Homotopy Continuation Methods

Homotopy continuation methods operate in two stages. Firstly, homotopy methods exploit the structure of P to find a root count and to construct a start system $P^{(0)}({\bf x}) = {\bf0}$that has exactly as many regular solutions as the root count. This start system is embedded in the homotopy

$$H({\bf x},t) = \gamma(1-t)P^{(0)}({\bf x}) + t P({\bf x}) = {\bf0}, \quad t \in [0,1],$$ (7)

with $\gamma \in {\Bbb C}$ a random number. In the second stage, as t moves from 0 to 1, numerical continuation methods trace the paths that originate at the solutions of the start system towards the solutions of the target system.

The good properties we expect from a homotopy $H({\bf x},t) = {\bf0}$ are (borrowed from [64]):

1.

(triviality) The solutions for t=0 are trivial to find.

2.

(smoothness) No singularities along the solution paths occur.

3.

(accessibility) All isolated solutions can be reached.

Continuation or path-following methods are standard numerical techniques ([3,4,5], [71], [123,125]) to trace the solution paths defined by the homotopy using predictor-corrector methods. The smoothness property of complex polynomial homotopies implies that paths never turn back, so that during correction the parameter t stays fixed, which simplifies the set up of path trackers. A pseudo-code description of a path tracker is in Algorithm 3.1.

The predictor delivers at each step of the method a new value for the continuation parameter and predicts an approximate solution of the corresponding new system in the homotopy. Figure 3 shows two common predictor schemes. The predicted approximate solution is adjusted by applying Newton's method as corrector. The third ingredient in path-following methods is the adaptive step size control. The step length is determined to enforce quadratic convergence in the corrector to avoid path crossing.

Algorithm 3.1   Following one solution path by an increment-and-fix predictor-corrector method with an adaptive step size control strategy.

Input: $H({\bf x},t)$, ${\bf x}^* \in {\Bbb C}^n$: $H({\bf x}^*,0) = {\bf0}$,		homotopy and start solution
$\epsilon > 0$, $max\_it$, $max\_steps$.		accuracy and upper bounds
Output: ${\bf x}^*$, success if $\vert\vert H({\bf x}^*,1)\vert\vert \leq \epsilon$.		approximate solution if success
t := 0; k := 0;		initialization
$h := max\_step\_size$;		step length
$old\_t := t$; $old\_{\bf x}^* := {\bf x}^*$		back up values for t and ${\bf x}^*$
$previous\_{\bf x}^* := {\bf x}^*$;		previous approximate solution
stop := false;		combines stopping criteria
while t < 1 and not stop loop
$t := \min(1,t + h)$;		secant predictor for t
${\bf x}^* := {\bf x}^* + h ( {\bf x}^* - previous\_{\bf x}^* )$;		secant predictor for ${\bf x}^*$
Newton( $H({\bf x},t),{\bf x}^*,\epsilon,max\_it$,success);		correct with Newton's method
if success		step size control
then $h := \min(Expand(h),max\_step\_size)$;		enlarge step length
$previous\_{\bf x}^* := old\_{\bf x}^*$;		go further along path
$old\_t := t$; $old\_{\bf x}^* := {\bf x}^*$;		new back up values
else h := Shrink(h);		reduce step length
$t := old\_t$; ${\bf x}^* := old\_{\bf x}^*$;		step back and try again
end if;
k := k+1;		augment counter
stop := ( $h < min\_step\_size$) or ( $k > max\_steps$);		stopping criteria
end loop;
success := ( $\vert\vert H({\bf x}^*,1)\vert\vert \leq \epsilon$).		report success or failure

Following all paths can be done sequentially, one path at a time, or in parallel, with for each solution path the same sequence of values of the continuation parameter. The sequential path-following method has the advantage that the low overhead of communication [6] makes it very suitable to run on multi-processor environments. Note that the memory requirements are optimal.

  

Figure 3: The secant and tangent predictor with step length h.

To solve repeatedly a polynomial system with the same coefficient structure $P({\bf c},{\bf x}) = {\bf0}$, the homotopy (7) is applied with $P^{(0)} = P({\bf c}^0,{\bf x}) = {\bf0}$ a system with random coefficients ${\bf c}^0$. Solving $P({\bf c}^0,{\bf x}) = {\bf0}$ is no longer trivial, so the name cheater's homotopy [57] is appropriate. A similar idea appeared in [75,76]. For coefficients given as functions of parameters, a refined version of cheater's homotopy in [59] avoids repeated evaluation of those functions during path following:

$$H({\bf x},t) = P((1-[t-t(1-t) \gamma]){\bf c}^0 + (t-t(1-t... ...c},{\bf x}) = {\bf0}, \quad t \in [0,1], \gamma \in {\Bbb C}.$$ (8)

In [59] it is proven that with (8) all isolated solutions of  $P({\bf c},{\bf x}) = {\bf0}$ can be reached and that singularities can only occur at the end of the paths.

Typically, when using a cheater's homotopy, the computational effort spent towards the end of the paths often accounts for most of the work. The main numerical problem is then to distinguish irrelevant solutions at infinity from ill-conditioned but possibly meaningful solutions. End games [43], [77,78,79], [95] provide several procedures to approximate the winding number of a path. Recently, Zeuthen's rule was applied in [50] to determine numerically the multiplicity of an isolated solution. Multi-precision facilities are useful for evaluation of residuals and root refinement for badly scaled solutions.

In most applications, the polynomial systems have real coefficients and invite the use of real homotopies. In [11] it was conjectured and proven in [60] that generically, real homotopies contain no singular points other than a finite number of quadratic turning points. At those bifurcation points pairs of real solution paths become imaginary or conversely, complex conjugated solution paths join to yield two real solution paths. We refer to [2], [38], [64] and [60,61] for a discussion of numerical techniques to deal with quadratic turning points. A remarkable application of real homotopies in the real world consists in the finding of the relevant parameters of a polynomial system to maximize the number of real roots, see [18] for the 40 real solutions for the Stewart-Gough platform in mechanics.

In [93] the use of homotopy continuation to deal with overdetermined and components of solutions is discussed. Geometrically one slices the components of solutions with as many random hyperplanes as the dimension of the components. The solutions to the original polynomial system augmented with these random linear equations for the hyperplanes are generic points of the components, constituting the main numerical data to study those components. In particular, the number of generic points one obtains by this slicing procedure equals the sum of the degrees over all top-dimensional components of solutions.

To make the algorithms of [93] more efficient, in [94], the following embedding of the polynomial system  $P({\bf x}) = {\bf0}$is proposed:

$$\left\{ \begin{array}{rl} p_i({\bf x}) + \lambda_i z = 0,... ...isplaystyle \sum_{j=1}^n c_j x_j + z = 0} \end{array} \right.$$ (9)

where the $\lambda_i$'s and c_j's are random complex numbers. This embedding has the advantage over the algorithms in [93] that fewer solution paths diverge. Solutions to the system (9) with z = 0 lie on a component of solutions. By Bertini's theorem, all solutions with $z \not= 0$ are regular. In [94], it is proven that those solutions can be used as start solutions to reach all isolated solutions of the original polynomial system  $P({\bf x}) = {\bf0}$.

The embedding (9) is performed repeatedly in the routine `Embed' in the algorithm (copied from [94]) below.

Algorithm 3.2   Cascade of homotopies between embedded systems.

Input: P, n.		system with solutions in ${\Bbb C}^n$
Output: $({\cal E}_i,{\cal X}_i,{\cal Z}_i)_{i=0}^n$.		embeddings with solutions
${\cal E}_0 := P$;		initialize embedding sequence
for i from 1 up to n do		slice and embed
${\cal E}_i$ := Embed( ${\cal E}_{i-1},z_{i}$);		zi = new added variable
end for;		homotopy sequence starts
${\cal Z}_n$ := Solve( ${\cal E}_n$);		all roots are isolated, nonsingular, with $z_n \not= 0$
for i from n-1 down to 0 do		countdown of dimensions
Hi+1 := $t {\cal E}_{i+1} + (1-t)\left( \begin{array}{c} {\cal E}_i \\ z_{i+1} \end{array} \right)$;		homotopy continuation $t: 1 \rightarrow 0$ to remove zi+1
${\cal X}_i$ := limits of solutions of Hi+1
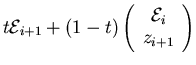as $t\to 0$ with zi=0;		on component
${\cal Z}_i$ := $H_{i+1}({\bf x},z_{i} \not= 0,t=0)$;		not on component: these solutions
		are isolated and nonsingular
end for.

This embedding allows the efficient treatment of overdetermined systems and other nonproper intersections. By perturbing the added hyperplanes and extending the generic points by continuation, interpolation methods can lead to equations for the components.